You will find several Demon face symbols (Picture on the right side) on the mountain walls across Watatsumi Island in Inazuma Region. These symbols are actually made by a Treasure Hoarding Pirate named Rinzou. These symbols are the locations where Rinzou stored his treasures. There are a total of 8 Rinzou mask symbols in Watatsumi. Finding the eight treasures unlocks the ‘Long John Silver’ achievement.
This article shows the location of all the eight Rinzou masks and how to get Rinzou’s treasure.

Treasure Hoarder’s Note Location
To get Rinzou’s treasures you will first need to complete Granny Komaki’s world quest and her Day 1 Challenge. Then get the Day 2 challenge from her. As part of the Day 2 challenge, find and read Treasure Hoarder’s Note. You will find the note inside a small cave in the southwest portion of Watatsumi Island as shown in the picture below. The note tells that a Pirate named Rinzou has hidden treasure at various locations in Watatsumi island. Once you have read the note, you will be able to dig the ground below Rinzou face symbols to get the treasure.
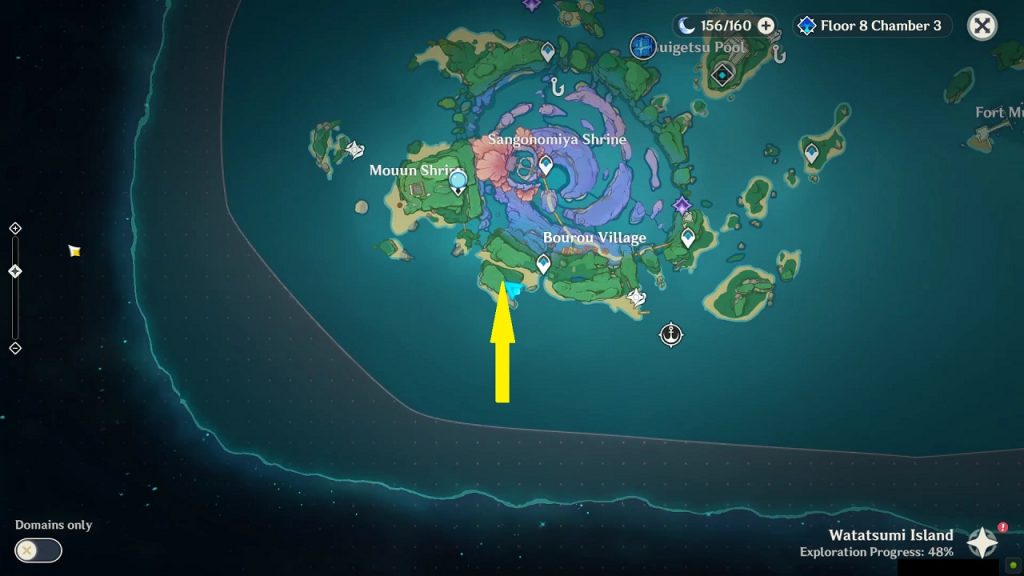

Rinzou Face Symbol 1/8
This symbol is on the mountain wall east side of Mouun Shrine at the location as shown in the picture below. Dig below the mask to get the treasure.

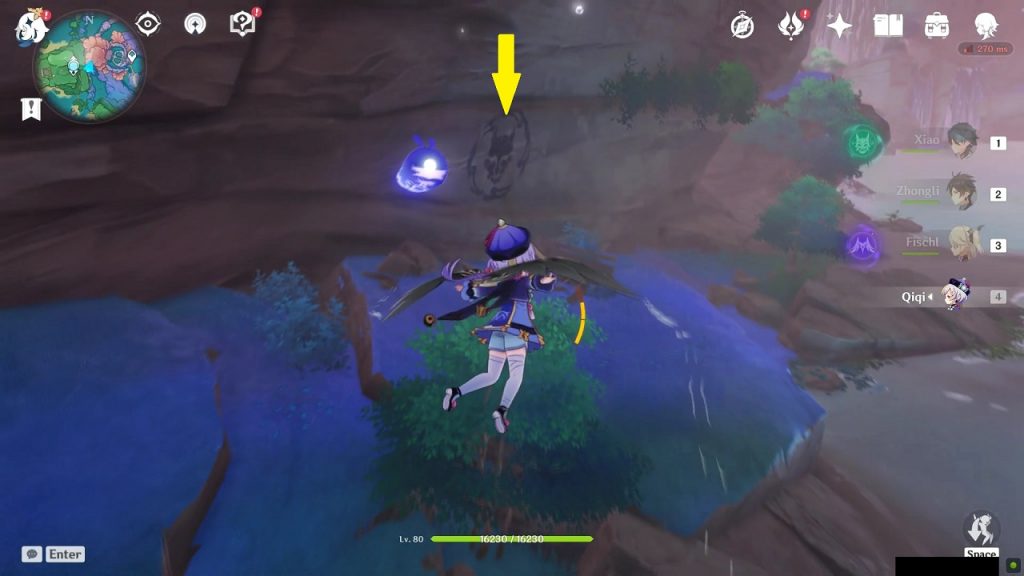
Rinzou Face Symbol 2/8
This symbol is on the mountain wall northeast side of Sangonomiya Shrine at the location as shown in the picture below. Dig below the mask to get the treasure.
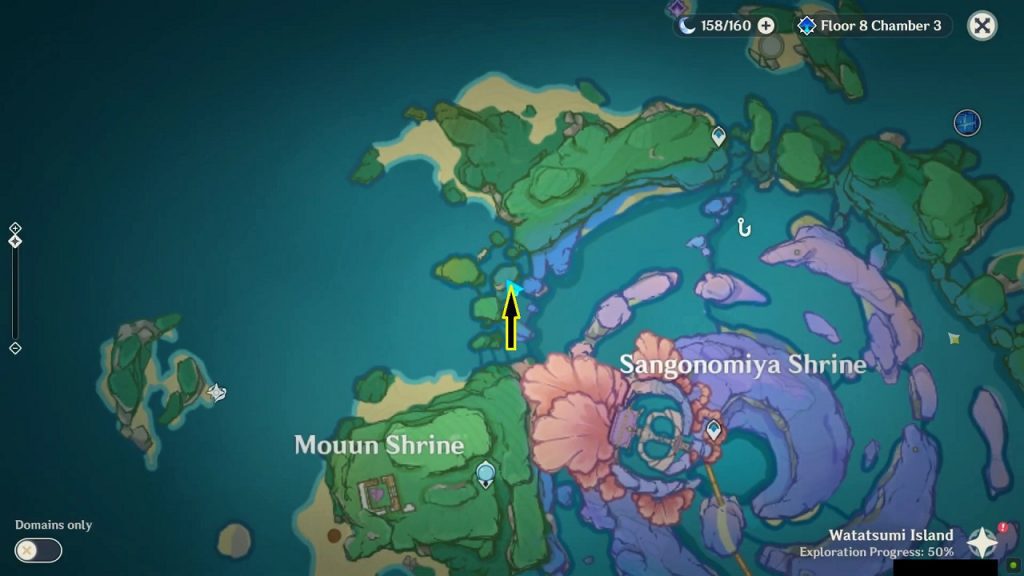

Rinzou Face Symbol 3/8
This symbol is on the mountain wall on the north of Sangonomiya Shrine at the location as shown in the picture below. Jump down from the mountain top and drop one level below to find the symbol and get the treasure.
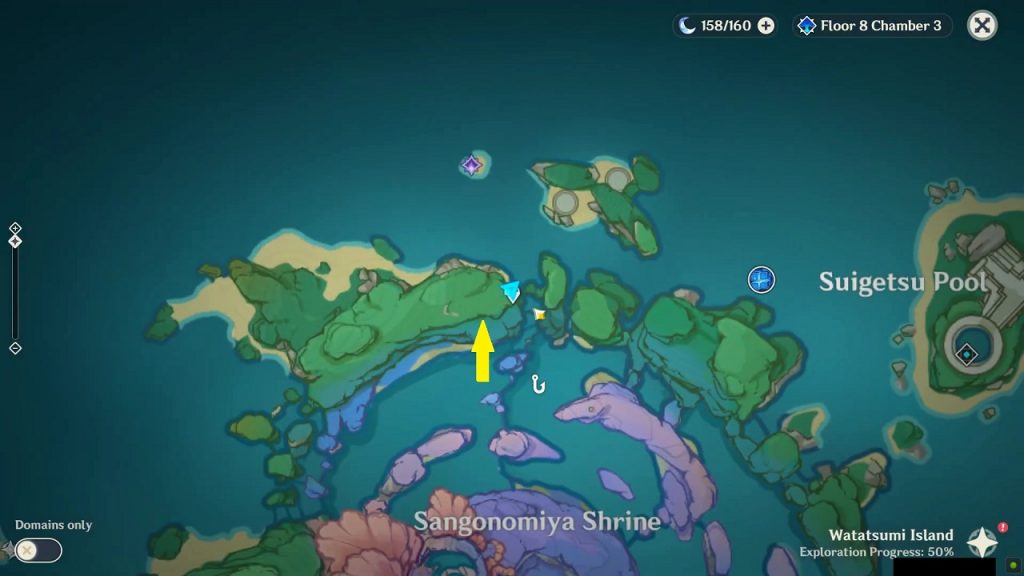

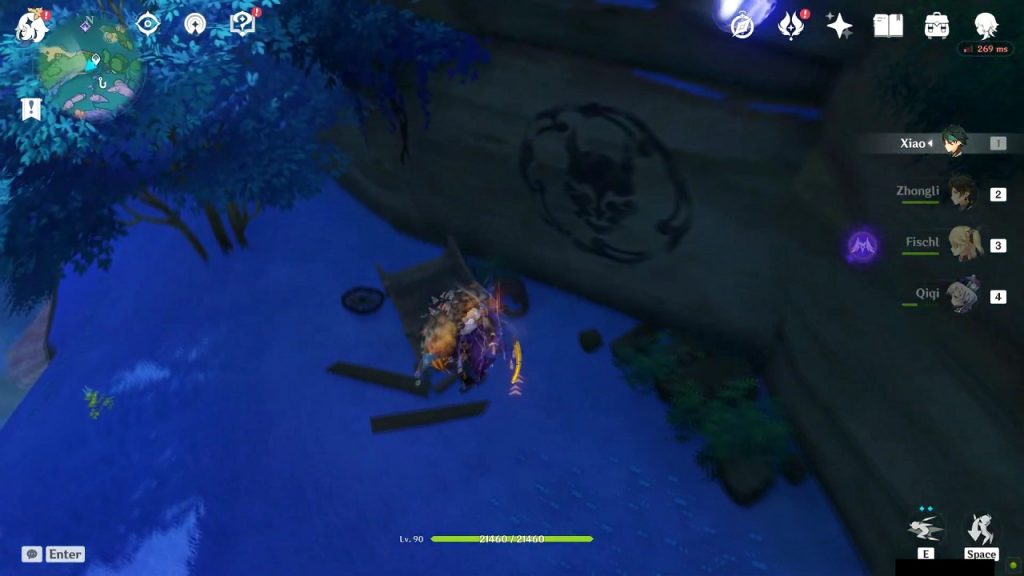
Rinzou Face Symbol 4/8
This symbol is on the mountain wall on the north of Sangonomiya Shrine at the location as shown in the picture below. Dig below the mask to get the treasure.
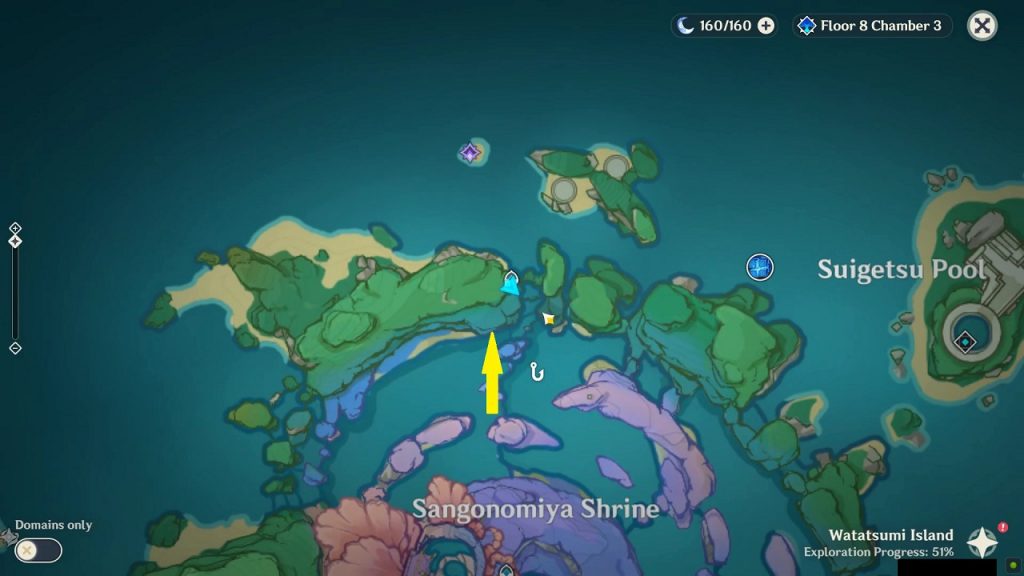

Rinzou Face Symbol 5/8
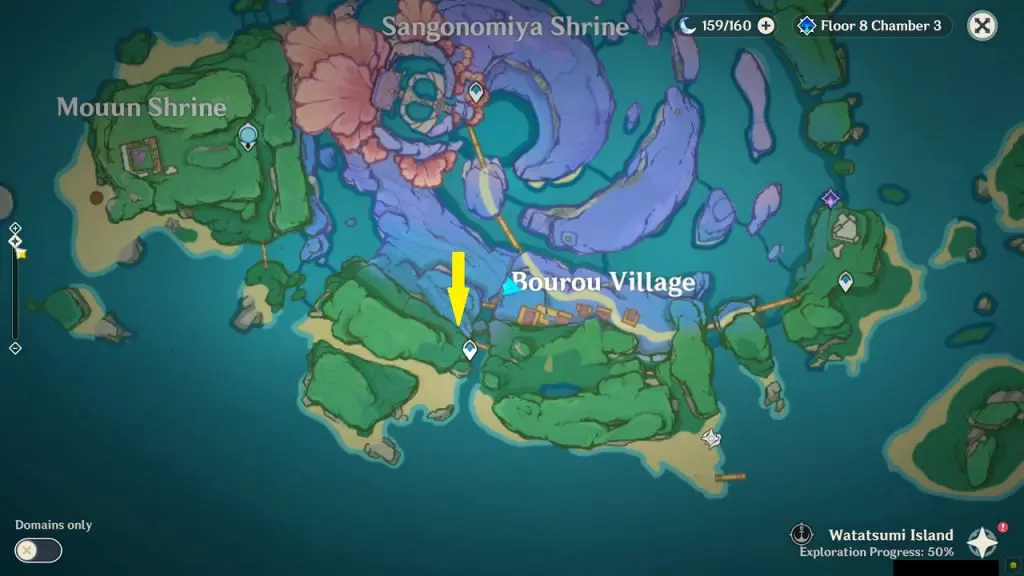
This symbol is on the mountain wall west of Bourou Village at the location as shown in the picture below. Dig below the mask to get the treasure.
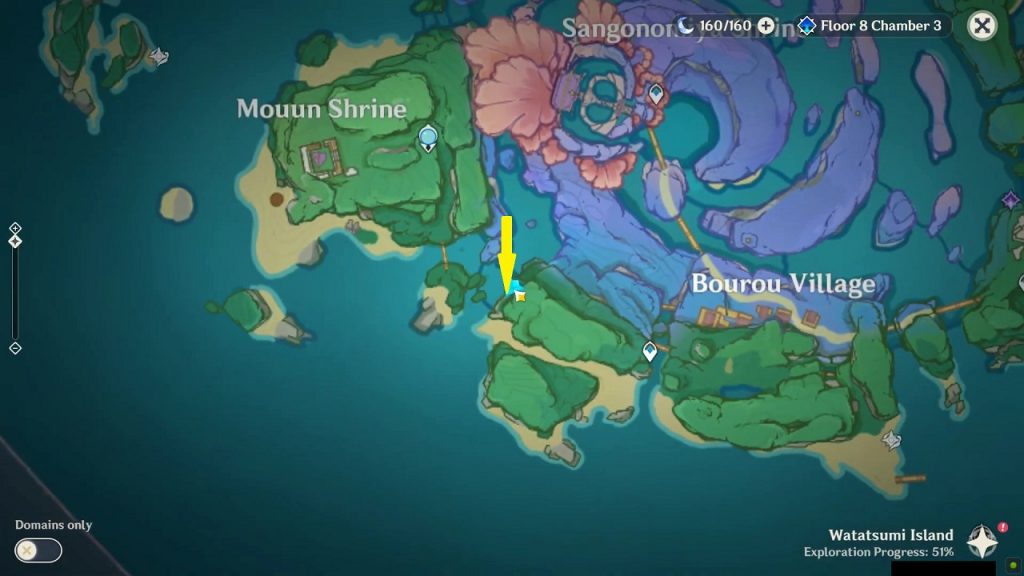
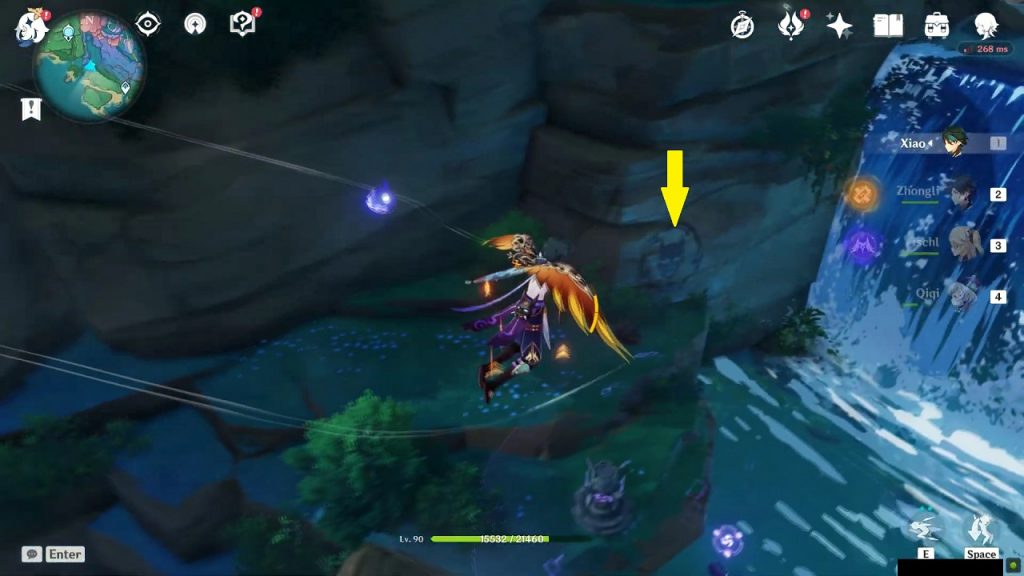
Rinzou Face Symbol 6/8
This symbol is on the mountain wall west of Bourou Village at the location as shown in the picture below. Walk over the wooden bridge west of the village and you will find the symbol in front of you. Dig below the mask to get the treasure.

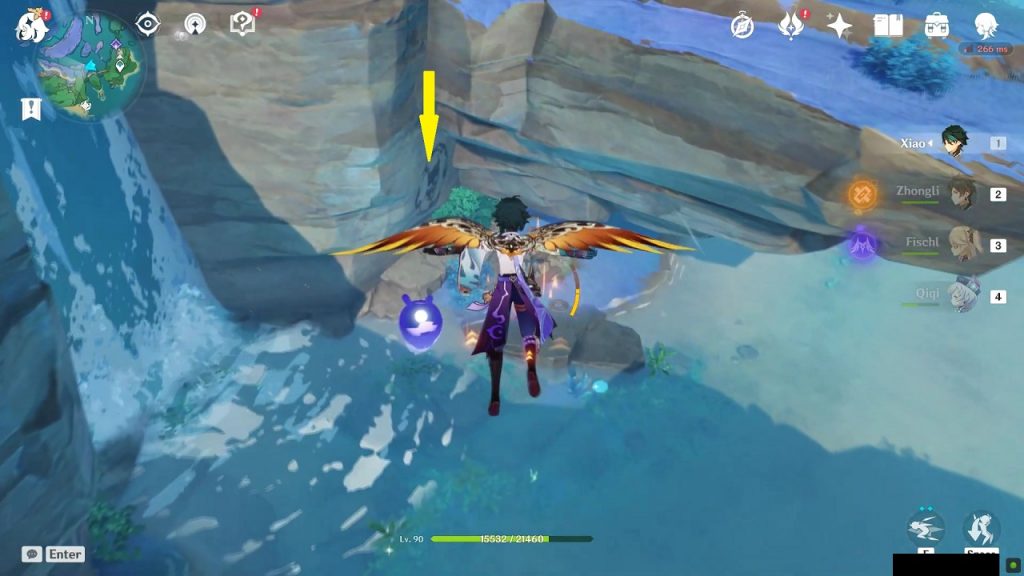
Rinzou Face Symbol 7/8
This symbol is on the mountain wall on the east side of Bourou Village at the location as shown in the picture below. Dig below the mask to get the treasure.

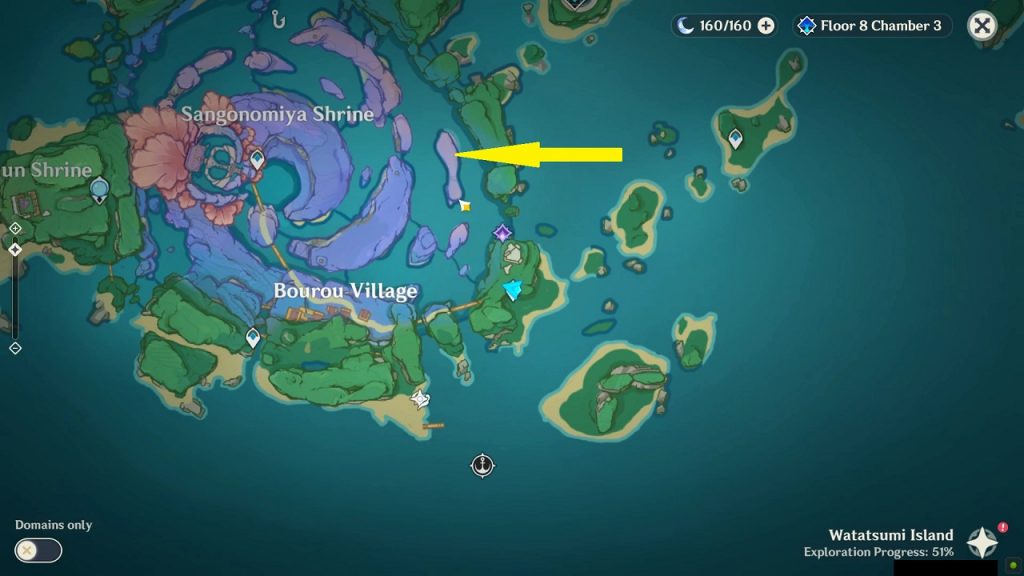
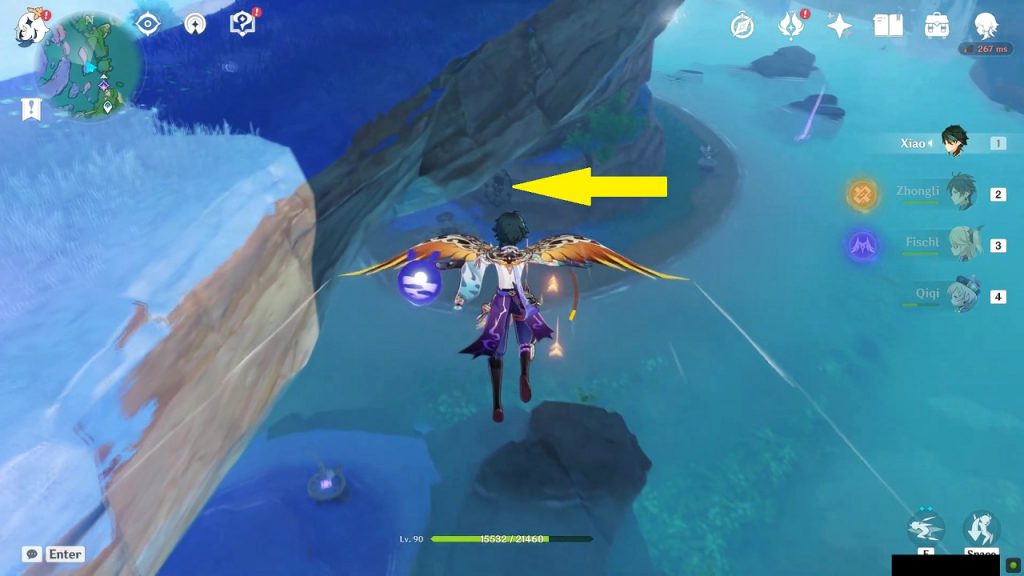
Rinzou Face Symbol 8/8
This symbol is on the mountain wall on the east side of Sangonomiya Shrine at the location as shown in the picture below. Dig below the mask to get the treasure.
You are not done yet. Another hidden achievement “A Distant Sea Shepherd’s Treasure” is also linked to the Treasure Hoarder’s Note. Click here to see how to unlock “A Distant Sea Shepherd’s Treasure” achievement.